ナンデモ解決！勉強ブログ

個人的に大好きな公式

ガウス積分

（理系大学生で理学部出身はほぼ全員学ぶはず？）

数Ⅲで学ぶ極座標

だったり、

数Ⅲで学ぶ部分積分や変換をしたり・・・

大学数学で学ぶ

2重積分をしたり・・・

今回は、

得てして数学が得意な人はなぜ得意か？

と言うお話をしていきたいと思います！！

結論

暗記数学を絶対にしたい人

です👌

もっと具体的に表現すると、

・公式を覚えるのではなく証明しに行く人

・あれかも？これかも？トライ&エラーを楽しむ人

個人的な考えですが、

間違っていない自信があります🎉

公式を覚えて使おうとする人は

暗記数学です😨

暗記数学は

定期テストや基本問題はできても、

より抽象的な問題や応用問題になったら

覚えていないので全くできなくなります😖

公式がなぜその公式になるのか？

そこにたどり着くまでには、

既習分野の内容をあれよこれよと駆使して、

初めて証明されます👀

このあれよこれよの部分が

数学的センスを身に付けるために

必要な過程なのです🎶

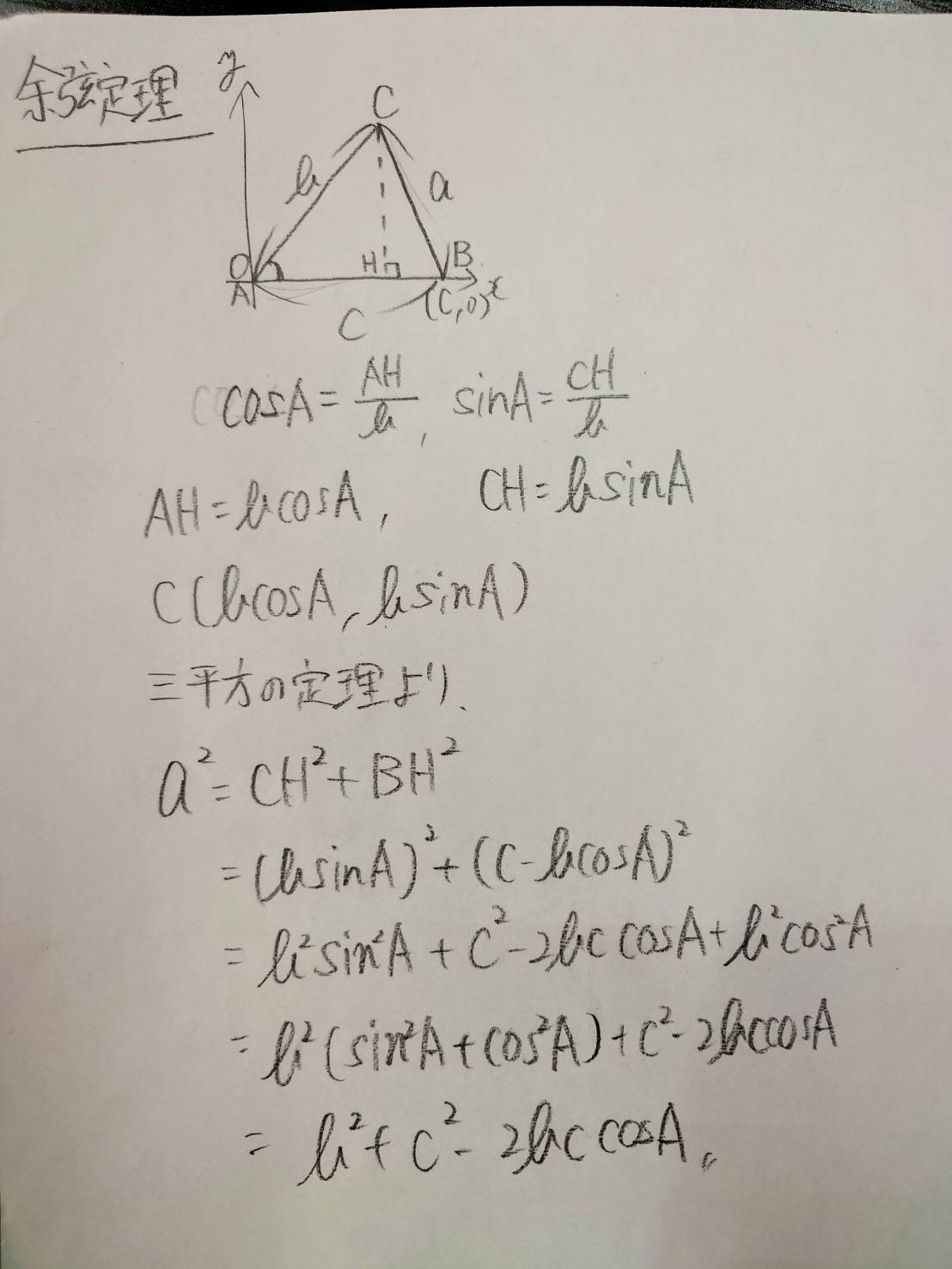
数学Ⅰの三角比で学ぶ

余弦定理

なぜ成り立つの？？

三角形をこうやって定義して・・・

と具体的にその過程を楽しめるようになると

非常に数学的センスは身に付きます！！

他にも・・・

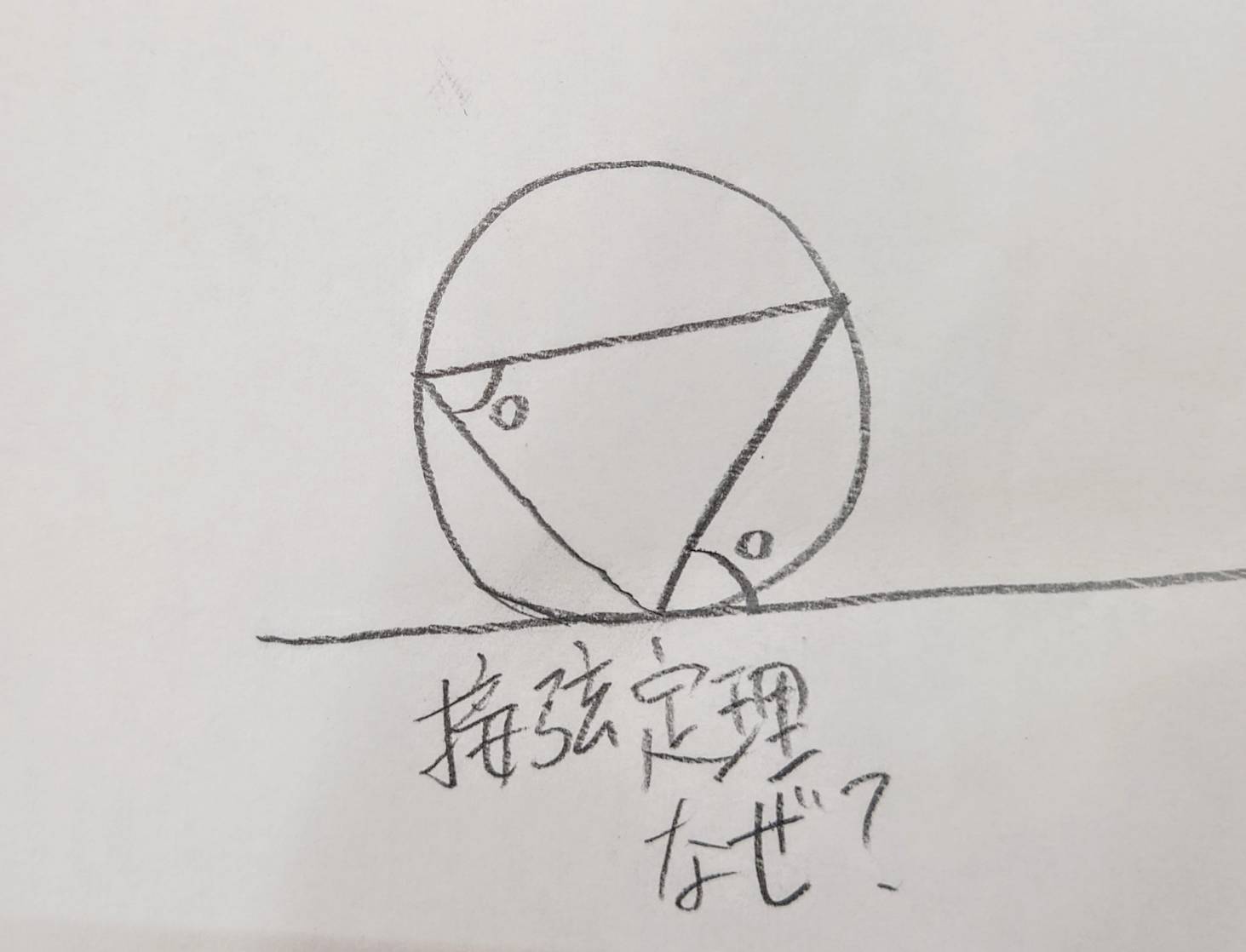
接弦定理ってなぜ成り立つの？

シグマの公式はなぜ成り立つの？？

となぜを解明しにいきましょう🙆‍♂️

そして、

図形の問題や文章題でも、

最初から諦めずに

色々とトライ&エラーをしていきましょう👌

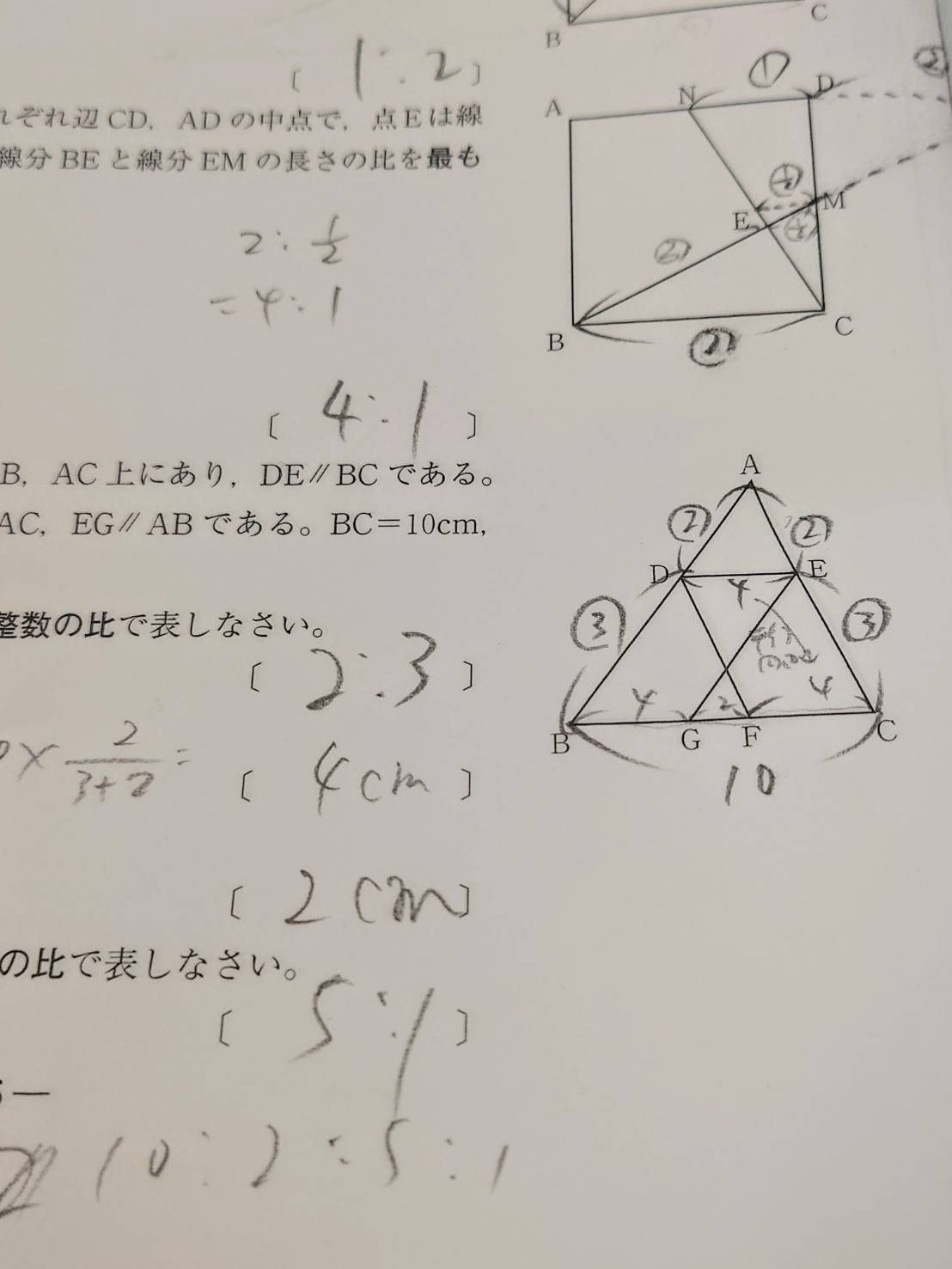
ここに補助線を引いてみようかな？

これとそれは相似が成り立つのでは？

三平方の定理か相似？もしくは図形の性質などで長さが求まる？

など、仮説を立てたうえで、

色々と試してみる！！

これも数学的センスが育まれる方法の1つです😌

何度も言いますが、

最初から

数学を暗記的に解こうとするのはNGです🙆‍♂️

たくさん問題を解いてしまい、

結果、

解き方を暗記してしまっているは

情報処理の観点では非常に大事ですが、

本来の数学力は身に付けられません😫

じっくりと大問1つを

30分かけて証明するような理系的な問題では、

真の数学力が必要です👍

公式がなぜ成り立つ？

色々と試してみる！

の精神で数学的センスを作り上げていきましょう😉

P.S

マクスウェル方程式という

大学で物理系学科の方は必修で学ぶ

物理公式も結構好きです😉